Lessons learned from the 2025 7th Grade Math STAAR

Aaron Daffern
4 days ago
6 min read

Using a modified version of the statewide item analysis report, I examined the readiness standards that had less than 60% mastery. Each standard has both an analysis of the items themselves to infer what made them so difficult and instructional implications for educators to ensure a more successful 2026 STAAR test.

Standard	# of items	% mastery
7.3B	2	38
7.9C	2	38.5
7.4D	2	42
7.11A	2	44
7.6G	2	44.5
7.9A	2	44.5
7.6I	2	46.5
7.7A	2	46.5
7.5C	2	48
7.9B	2	49.5
7.4A	2	55.5
7.12A	2	57.5

Access the slide deck here.

7.3B - 38% overall mastery

apply and extend previous understandings of operations to solve problems using addition, subtraction, multiplication, and division of rational numbers

#11 - 27% correct

#36 - 49% correct

Analysis

#11 was mainly guessing, answers received between 21% - 27%
Students most likely stumbled when multiplying the mixed number by the whole number
For #36, 23% chose B [(11.75 + 18.36) - 0.1(11.75 + 18.36)]

Instructional Implications

Both problems involved mixed numbers/fractions, reinforcing need for students to be comfortable changing between fractions and decimals
Surprisingly, students did much better on the word problem (#36) with the hidden operation of multiplication (i.e., discount)

7.9C - 38.5% overall mastery

determine the area of composite figures containing combinations of rectangles, squares, parallelograms, trapezoids, triangles, semicircles, and quarter circles

#12 - 27% correct

#22 - 50% correct

Analysis

#12 involved two different shapes while #22 involved only rectangles
To solve #12, students had to use the term “congruent” to find the missing dimensions
#12 could have been manipulated into one rectangle by rotating and translating the bottom triangle

Instructional Implications

Encourage students to look for simpler problems (e.g., make a new shape by rearranging the existing shapes)
Practice should emphasize finding missing side lengths using deduction

Watch the full walkthrough of all 38 items on the 2025 7th Grade STAAR below.

7.4D - 42% overall mastery

solve problems involving ratios, rates, and percents, including multi-step problems involving percent increase and percent decrease, and financial literacy problems

#7 - 33% correct

#38 - 51% correct

Analysis

Students had more difficulty with percent increase (#7) than a basic rate problem (#38)
For #7, 35% chose A (15 - 12 rather than (15 - 12)/12)
For #38, 23% chose A (45 / 8)

Instructional Implications

Recognition of the type of problem (percent increase/decrease vs ratio/rate) is the first step in solving these types of problems
If the latter, students need time and practice to recognize when to solve for a unit rate (if needed) and when to set up a proportion

7.11A - 41% overall mastery

model and solve one-variable, two-step equations and inequalities

#16 - 37% correct

#33 - 51% correct

Analysis

Students had to navigate the directionality of inequality on #16, derived from a word problem, while #33 was a straightforward equation
For #16, 28% chose C (wrong direction of inequality)
#33 required combination of like terms

Instructional Implications

The two largest challenges with inequalities and verbal descriptions are:
- Identifying the correct symbol from the context of the word problem
- Flipping the inequality when multiplying or dividing by a negative
Have students work out some of the x- and y-values for word problems and then plug them back in to check their work

7.6G - 42% overall mastery

solve problems using data represented in bar graphs, dot plots, and circle graphs, including part-to-whole and part-to-part comparisons and equivalents

#15 - 36% correct

#30 - 53% correct

Analysis

#15 required students to evaluate four separate statements while #30 required one calculation
For #15, 24% chose B and 24% chose C, indicating guessing

Instructional Implications

By 7th grade, students’ work with graphs will come down to finding the percent or fraction the amounts shown
By turning each statement to evaluate (#15) into a number sentence, students can more easily evaluate them

7.9A - 44.5% overall mastery

solve problems involving the volume of rectangular prisms, triangular prisms, rectangular pyramids, and triangular pyramids

#5 - 36% correct

#26 - 53% correct

Analysis

Both problems gave complete models and asked students to find the volume (as opposed to giving volume and base and asking for height)
For #5, 34% chose C (forgot to multiply by ½ when calculating area of base)
For #26, 20% chose D (forgot to multiply by ⅓)

Instructional Implications

These calculations require basic use of formula
Work with students to use the commutative property of multiplication to make simpler problems first

7.6I - 46.5% overall mastery

determine experimental and theoretical probabilities related to simple and compound events using data and sample spaces

#13 - 60% correct

#24 - 33% correct

Analysis

Students did not struggle with simple events (#13) as much as they did with compound events (#24)
For #13, 21% chose C (yellow and green are 2 choices out of 5)
For #24, 30% chose B (any card was 1/40, thus 1/40 + 1/40 = 2/40 = 1/20)

Instructional Implications

The first step in solving probability is to classify the problem as a simple or compound event
Students should have practice with compound events with the same and different denominators

7.7A - 46.5% overall mastery

represent linear relationships using verbal descriptions, tables, graphs, and equations that simplify to the form y = mx + b

#9 - 63% correct

#21 - 11% full credit; 35% partial credit; 54% no credit

Drop-down 1: -3; -2; 3; 5

Drop-down 2: -4; 0; 3; 5

Analysis

Students found little challenge with #9, though 17% still chose B (increase rather than decrease)
#21 had a clear y-intercept (5) and at least 4 usable coordinates
If all 35% partial credit correctly entered the y-intercept, that’s still only 46%

Instructional Implications

Identifying key features is still a struggle for students in Algebra I and get more challenging as x-intercepts (i.e., zeros, solutions) are introduced later
Show students how to calculate slope when given a graph without using the slope formula (rise/run)

7.5C - 48% overall mastery

solve mathematical and real-world problems involving similar shape and scale drawings

#10 - 41% correct

#20 - 55% correct

Analysis

Students might have found the map diagram unique and possibly confusing
For #10, a rough estimate of 150 / 25 * 0.5 would have found 3 in
The incorrect answer choices for #20 were closely distributed (12% - 18%)
Reasoning could have eliminated A and B for #20

Instructional Implications

Emphasize labeling units when setting up proportions
Have students use reasoning to eliminate answer choices

7.9B - 49.5% overall mastery

determine the circumference and area of circles

#8 - 21% full credit; 36% partial credit; 43% no credit

#29 - 60% correct

Analysis

#8 requires students to navigate both area and circumference of a circle
Given the diameter, students needed to calculate the radius (no formula given)
#29 uses the standard equation C = πd

Instructional Implications

The relationship between radius and diameter can be derived from the formulas for circumference
- C = πd
- C = 2πr
Since students had to calculate without technology and the answer choices did not include decimals, estimation would have been appropriate

7.4A - 55.5% overall mastery

represent constant rates of change in mathematical and real-world problems given pictorial, tabular, verbal, numeric, graphical, and algebraic representations, including d = rt

#4 - 64% correct

#31 - 47% correct

Analysis

#4 intermixed equations and tables, given rate was not represented
The large numbers used in #31 might have thrown students off
21% of students chose C (thought the unit rate was given)

Instructional Implications

The initial step is to recognize problem situations that describe a constant rate of change
Students should be comfortable multiplying and dividing by multiples of 10, 100, or 1,000

7.12A - 57.5% overall mastery

compare two groups of numeric data using comparative dot plots or box plots by comparing their shapes, centers, and spreads

#17 - 55% correct

#34 - 39% full credit; 42% partial credit; 19% no credit

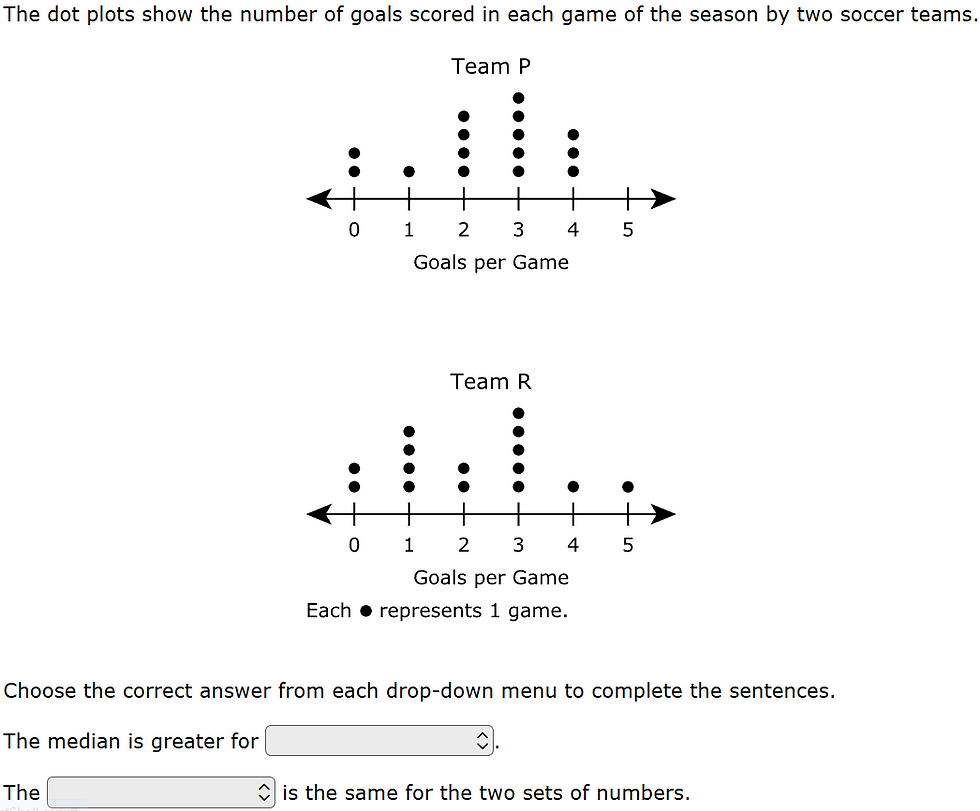
Drop-down 1: team P; team R

Drop-down 2: mode; range; maximum

Analysis

#17 required students to evaluate range, IQR, distribution, and median
#34 required students to evaluate mode, range, maximum (answer choices for drop-down #2) and median
24% chose C

Instructional Implications

Students should be well-versed in measures of center (median, mean), measures of spread (range, IQR), and the shape (e.g., symmetry) of data representations
As stated in the TEKS, this standard is about comparing two sets of data